Un blog para las clases de Educación Plástica, Visual y Audiovisual, bilingües de 2º de E.S.O.... y más. Vuestro blog, vuestros trabajos, vosotros.
Páginas
- BLOG: Pág. Principal
- Students freetime Gallery
- Un viaje para tod@s
- London Corner
- Endicott Corner (Beverly, Boston, MA)
- ART VOCABULARY
- ART GRAMMAR
- Irish ART
- Californian ART
- Wisconsin ART
- Australian ART
- Virgin Islands ART
- North Carolina Art
- Native American ART
- Texas ART
- Hindu ART
- Art Movements
- Art - Pillow face
- Art - Artistopoly
- Lesson Plans
- CLIL-AICLE
- PLASTI-PLE
- TUTORÍAS ESO
- Art and Maths
- Encuesta final curso
- Evaluación y Criterios de Calificación EPVA
- Contactar con la profe
Thursday 30 June 2016
My favourite notebook
My favourite notebook on PhotoPeach
Wednesday 29 June 2016
Reviewing Basic Constructions for your Visual Arts exam
A review for the exam (with videos in Spanish)
Don't just watch the videos. Do it yourself using your set squares and compass!
Dividing a line segment into equal parts:
Symmetry of a shape:
Line segments operation (adding up and subtracting):
Perpendicular bisector:
Move or copy an angle:
Angles operation (adding up):
Angles operation (subtracting):
Angle bisector:
Square given a side
Square inscribed in a circumference
Equilateral triangle inscribed in a circumference (given the radius of the circumference)
Equilateral triangle given the side
Circumference through 3 points
Don't just watch the videos. Do it yourself using your set squares and compass!
Dividing a line segment into equal parts:
Symmetry of a shape:
Line segments operation (adding up and subtracting):
Perpendicular bisector:
Move or copy an angle:
Angles operation (adding up):
Angles operation (subtracting):
Angle bisector:
Square given a side
Square inscribed in a circumference
Equilateral triangle inscribed in a circumference (given the radius of the circumference)
Equilateral triangle given the side
Circumference through 3 points
Monday 27 June 2016
Parallel and Perpendicular lines, again!
Take a look to this presentation to review how to create parallel and perpendicular lines, and do the task.
Saturday 18 June 2016
The Circumference
Angle Bisector
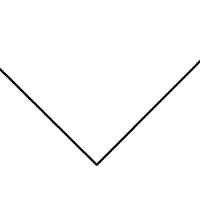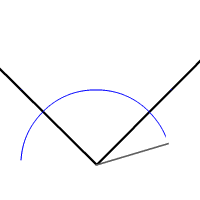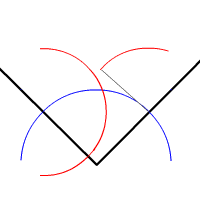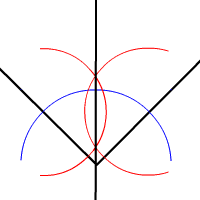
BISECT AN ANGLE
To bisect an angle means that we divide the angle
into two equal parts without actually measuring the angle. Each point of an angle bisector is equidistant from the sides of the angle.
STEPS:
STEPS:
- Draw an angle.
- Center the compass at vertex of the given angle and draw an arc intersecting both sides of it. We get 1 and 2
- Center the compass at point 1 and draw an arc.
- With the same measure center it at point 2 and draw another arc.
- Where these arcs cross we get point 3.
- If we join point 3 with the vertex of the angle we get the angle bisector.
- Try it yourself. Bisecting an angle.
Thales Theorem
A very funny way of explaining Thales Theorem:
Dividing a segment into several equal parts
We use Thales theorem to divide a given line segment into a number of equal parts with
compass and straightedge or ruler. By using a compass and straightedge construction, we
do this without measuring the line.
STEPS:
- Draw the given segment AB. This is the segment that we want to divide.
- From point A draw an oblique ray (r).
- Chose a measure with your compass and from point A draw arcs on the oblique ray as many arcs as parts you need.
- Join the last point of the oblique ray with point B.
- Draw parallels using your set square to the segment B7 from the other points on the ray.
Here we have divided the segment in seven parts, but you can divide the segment in as many parts as you need.
I think my construction is easier, but here you have another construction. In the applet we divide it into five parts but it can be any number. You will discover that both are the same!.
Saturday 11 June 2016
Perpendicular bisector
See perpendicular bisector construction. This construction shows how to draw the perpendicular bisector of a given line segment with compass and straightedge or ruler.
This construction bisects the segment (divides it into two equal parts, and is perpendicular to it. 1
STEPS: 2
First of all we need to draw a segment. We call it PQ (it could have been given).
First of all we need to draw a segment. We call it PQ (it could have been given).
- Center your compass in point P, open it further from the middle of the segment PQ, and draw an arc.
- Do the same from point Q, where these arcs cross each other we get points 1 and 2.
- Join 1 and 2, and this way we will get the line bisector of segment PQ.
Saturday 4 June 2016
Angles. Angles operations
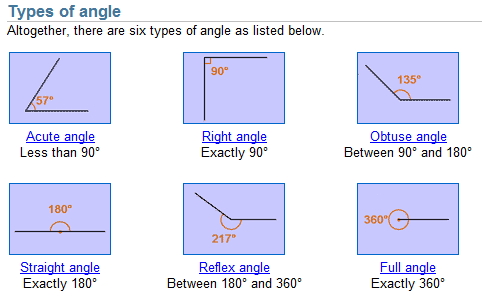
ANGLES
Definition: A shape, formed by two lines or rays diverging from a common point (the vertex).
Parts: vertex, legs (rays), interior, exterior.
TYPES OF ANGLES
Animation.
COPYING OR TRANSLATING AN ANGLE
In Geometry, "translation" simply means moving without rotating, resizing or anything eles, just moving.
STEPS:
This page shows how to copy an angle. Given an angle formed by two lines with a common vertex, this animation shows how to
construct another angle from it that has the same angle measure using a compass
and straightedge or ruler.Definition: A shape, formed by two lines or rays diverging from a common point (the vertex).
Parts: vertex, legs (rays), interior, exterior.
 |
| A triangle has three vertex |
Animation.
COPYING OR TRANSLATING AN ANGLE
In Geometry, "translation" simply means moving without rotating, resizing or anything eles, just moving.
STEPS:
- Center the compass at vertex of the given angle and draw an arc intersecting both sides of it. Without changing the radius of the compass, center it at point V and draw another arc
- Set the compass radius to the distance between the two intersection points of the first arc.
- Now center the compass at the point where the second arc intersects ray V.
- Mark the arc intersection point 1.
- Join point V with point 1 so you get the equal angle.
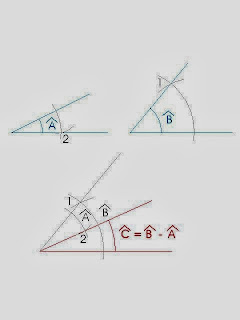
ADDING UP ANGLES
The addition of two angles is another angle whose measure is the addition of the measures of those two angles.
STEPS:- Copy angle A using translation of an angle.
- From this new angle copy angle B.
- The solution is angle C.
The subtraction of two angles is another angle whose measure is the subtraction of the measures of those two angles.
STEPS:- Copy angle B (the biggest one) using translation of an angle.
- From this new angle copy angle A.
- The solution is angle C.
- Try it yourself. Copying an angle.
Thursday 2 June 2016
Line segment operations
COPYING A LINE SEGMENT
This page shows how to copy a line segment with compass and straightedge or ruler. Given a line segment, this shows how to make another segment of the same length.
This page shows how to copy a line segment with compass and straightedge or ruler. Given a line segment, this shows how to make another segment of the same length.
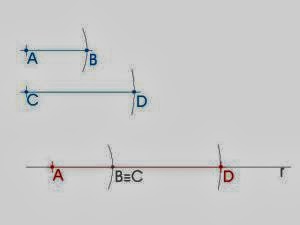
ADDING UP LINE SEGMENTS (in your notebooks)
The addition of two segments is another segment that begins at the origin of the first segment and ends at the end of the second segment.
STEPS:
- Draw a line (r).
- Draw a point A on it. (step 1 and 2 could be given)
- Measure the given segment AB with your compass.
- Draw an arc from A with that measure, so you get B.
- Measure the given segment CD with your compass.
- Draw an arc from B with that measure, so you get D.
- The solution is the segment AD.
SUBTRACTING LINE SEGMENTS (in your notebooks)
STEPS:
- Draw a line (r).
- Measure the longest segment with your compass, in our case is the segment CD.
- Draw a point C on r. (step 1 and 3 could be given)
- Draw an arc from dot C with the previous measure (the segment CD), so you get D.
- Measure the smallest segment with your compass, in our case is the segment AB.
- Draw an arc from D with that measure, so you get B.
- The solution is the segment CB.
Wednesday 1 June 2016
Parallel and perpendicular lines
How do we use the set square?
You have to handle your set square softly and with accuracy without exercising too much pressure on them, only the needed one to avoid movement.
PARALLEL LINES
- The 45 set square hypotenuse (longest side) is placed attached to the line to which we want to draw the parallels (GUIDE).
- The 60-30 set square hypotenuse is attached to the 45 set square leg.
- Fix the 60-30 set square and move the 45 set square upwards or downwards drawing the desired parallel lines along its hypotenuse.
PERPENDICULAR LINES
If we want to draw perpendicular lines to one direction, we will have to follow the first two steps as stated for parallel lines and then the following ones:
- Having fixed the 60-30 set square, the 45 set square is turned until the other leg is attached to the hypotenuse of the 60-30 set square.
- Draw the perpendicular line along the hypotenuse of the 45 set square.
Labels:
1st ESO,
basic geometry,
line,
tasks 2015-2016,
technical drawing
Subscribe to:
Posts (Atom)